Zawartość
W geometrii sześciokąt jest wielokątem o sześciu bokach. Zwykły sześciokąt ma sześć równych boków i równych kątów. Zwykły sześciokąt jest powszechnie rozpoznawany z plastra miodu i wnętrza Gwiazdy Dawida. Sześciokąt to sześciokątny wielościan. Zwykły sześciokąt ma sześć trójkątów o krawędziach równej długości. Innymi słowy, jest to sześcian.
Formuła powierzchni sześciokąta
Wzór na obszar regularnego sześciokąta o bokach długości „a” wynosi 3 --- sqrt (3) --- a ^ 2/2, gdzie „sqrt” oznacza pierwiastek kwadratowy.
Pochodzenie
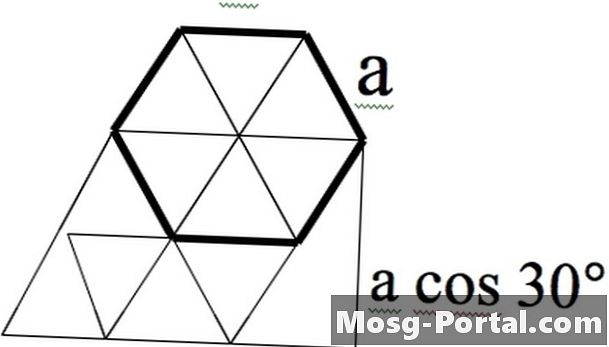
Zwykły sześciokąt można postrzegać jako sześć równobocznych trójkątów boków a. Ich kąty wynoszą 60 stopni, więc kąty w sześciokącie wynoszą 120 stopni. Trójkąty mogą być przedłużone poniżej sześciokąta, tworząc równoległobok boków 2a. Można określić większy trójkąt, aby określić wysokość tego równoległoboku, który wynosi 2a --- cos 30 ° = a --- sqrt (3).
Dlatego równoległobok na rysunku ma wysokość powierzchni --- podstawa = (a --- sqrt (3)) --- 2a = 2 --- sqrt (3) --- a ^ 2.
Ale dotyczy to równoległoboku złożonego z 8 trójkątów równobocznych. Sześciokąt składał się tylko z 6. Tak więc powierzchnia sześciokątów wynosi 0,75 tego lub 3 --- sqrt (3) --- a ^ 2/2.
Alternatywne pochodzenie
Sześć trójkątów równobocznych w sześciokącie ma boki „a”. Ich wysokości, h, według twierdzenia Pitagorasa, sqrt = a --- sqrt (3) / 2.
Obszar trójkąta wynosi zatem (½) --- podstawa --- wysokość = (a) ---. Sześć trójkątów w sześciokącie daje powierzchnię 3 --- sqrt (3) --- a ^ 2/2.
Formuła objętości sześciokąta
Wzór na objętość zwykłego sześciokąta boków „a” to ^ 3, ponieważ zwykły sześciokąt jest sześcianem.
Pole powierzchni wynosi oczywiście ^ 2 --- 6 boków = 6a ^ 2.