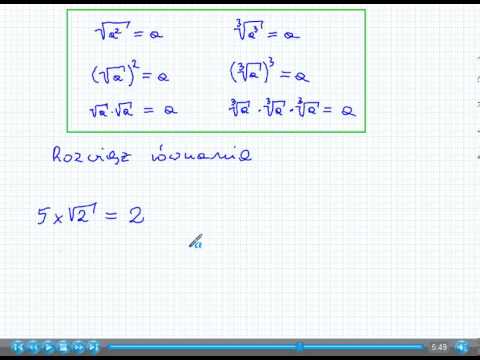
Manipulowanie pierwiastkami i wykładnikami jest jednym z podstawowych składników algebry. Będziesz musiał nauczyć się wykonywać operacje z korzeniami i wykładnikami w klasach algebry w szkołach średnich i wyższych, a także w dziedzinach kariery, które w dużym stopniu opierają się na matematyce, takich jak inżynieria. Aby manipulować pierwiastkami i wykładnikami, zapoznaj się z zestawem reguł algebraicznych.
Zrozum, że liczba lub zmienna pierwszej mocy pozostaje taka sama. Na przykład a ^ 1 = a.
Dodaj wykładniki, które mają tę samą podstawę w problemie mnożenia. Na przykład y ^ 3 x y ^ 4 = y ^ 3 + 4. Dlatego odpowiedź brzmi y ^ 7.
Pomnóż wiele wykładników należących do jednej bazy. Na przykład x ^ (2) (3) = x ^ 2x3, co równa się x ^ 6.
Odejmij wykładniki podobnych zasad w problemach z dzieleniem. Na przykład a ^ 5 / a ^ 2 = a ^ 5-2, co równa się ^ 3.
Uświadom sobie, że dowolna liczba lub zmienna podniesiona do zerowej mocy jest równa 1.
Potraktuj wykładniki ujemne w sposób wzajemny. Na przykład x ^ -3 = 1 / x ^ 3.
Podziel wykładniki, gdy w grę wchodzi znak root. Na przykład, jeśli po lewej stronie znaku pierwiastka kwadratowego jest wykładnik 2 i x ^ 3 pod znakiem pierwiastka kwadratowego, odpowiedzią byłoby x ^ 3/2.
Zrozum, że pierwiastek kwadratowy z dwóch zwielokrotnionych zmiennych jest równy iloczynowi każdej zmiennej do kwadratu. Na przykład pierwiastek kwadratowy z xy jest równy pierwiastkowi kwadratowemu z x razy pierwiastek kwadratowy z y.
Zrozum, że iloraz dwóch zmiennych pod znakiem pierwiastka kwadratowego jest równy pierwiastkowi kwadratowemu zmiennej górnej podzielonemu przez pierwiastek kwadratowy zmiennej dolnej. Na przykład pierwiastek kwadratowy z x / y jest równy pierwiastkowi kwadratowemu z x podzielonemu przez pierwiastek kwadratowy z y.