Trójkąt równoboczny jest trójkątem o wszystkich trzech bokach jednakowej długości. Pole powierzchni dwuwymiarowego wielokąta, takiego jak trójkąt, jest całkowitym obszarem zawartym po bokach wielokąta. Trzy kąty trójkąta równobocznego są również równe w geometrii euklidesowej. Ponieważ całkowita miara kątów trójkąta euklidesowego wynosi 180 stopni, oznacza to, że wszystkie kąty trójkąta równobocznego mierzą 60 stopni. Pole trójkąta równobocznego można obliczyć, gdy znana jest długość jednego jego boków.

Określ obszar trójkąta, gdy znana jest podstawa i wysokość. Weź dowolne dwa identyczne trójkąty o podstawie s i wysokości h. Zawsze możemy utworzyć równoległobok podstawy si wysokości h za pomocą tych dwóch trójkątów. Ponieważ obszar równoległoboku wynosi s x h, obszar A trójkąta wynosi zatem x s.

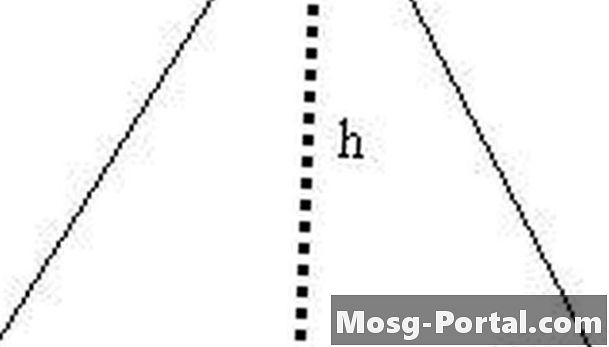
Utwórz trójkąt równoboczny w dwa trójkąty prawe za pomocą odcinka linii h. Przeciwprostokątna jednego z tych prostokątów o długości s, jedna z nóg ma długość h, a druga noga ma długość s / 2.
Express h w kategoriach s. Używając odpowiedniego trójkąta utworzonego w kroku 2, wiemy, że s ^ 2 = (s / 2) ^ 2 + h ^ 2 według wzoru pitagorejskiego. Dlatego h ^ 2 = s ^ 2 - (s / 2) ^ 2 = s ^ 2 - s ^ 2/4 = 3s ^ 2/4, a teraz mamy h = (3 ^ 1/2) s / 2.
Zamień wartość h uzyskaną w kroku 3 na wzór na pole trójkątów uzyskane w kroku 1. Ponieważ A = ½ sxh i h = (3 ^ 1/2) s / 2, mamy teraz A = ½ s (3 ^ 1/2) s / 2 = (3 ^ 1/2) (s ^ 2) / 4.
Użyj wzoru na pole trójkąta równobocznego uzyskanego w kroku 4, aby znaleźć obszar trójkąta równobocznego o bokach o długości 2. A = (3 ^ 1/2) (s ^ 2) / 4 = (3 ^ 1/2 ) (2 ^ 2) / 4 = (3 ^ 1/2).