Zawartość
- Co to jest trapez?
- Co to jest nieregularny trapez?
- Formuła pola trapezowego
- Jak obliczyć powierzchnię nieregularnego trapezu: podane wartości
- Jak obliczyć powierzchnię nieregularnego trapezu: Znajdowanie wysokości nieregularnego trapezu
Chociaż może się wydawać, że znalezienie obszaru o różnych kształtach i wielokątach ogranicza się do klasy matematycznej w szkole, faktem jest, że znalezienie obszaru wielokątów jest czymś, co dotyczy prawie wszystkich części życia. Od obliczeń rolniczych po zrozumienie obszaru określonego ekosystemu w biologii po informatykę, obliczanie obszarów o skomplikowanych kształtach jest niezbędną umiejętnością do opanowania.
Zwykle łatwiej jest zmierzyć powierzchnię kształtów o wszystkich równych bokach i prostych wzorach. Jednak „nieregularne” kształty, takie jak nieregularny trapez, znany również jako nieregularny trapez, są powszechne i należy je również obliczyć. Na szczęście istnieją kalkulatory nieregularnych obszarów trapezowych i formuła pola trapezowego, które upraszczają ten proces.
Co to jest trapez?
Trapez to czworoboczny wielokąt, znany również jako czworokąt, który ma przynajmniej jeden zestaw równoległych boków. To odróżnia trapez od równoległoboku, ponieważ równoległoboki zawsze mają dwa zestawy równoległych boków. Dlatego możesz uznać wszystkie równoległoboki za trapezoidy, ale nie wszystkie trapezoidy są równoległobokami.
Nazywa się równoległe boki trapezu zasady podczas gdy nazywane są nierównoległe boki trapezu nogi. Regularny trapez, zwany także trapezem równoramiennym, to trapez, w którym nierównoległe boki (nogi) mają równą długość.
Co to jest nieregularny trapez?
Nieregularny trapez, zwany również nieregularnym trapezem, jest trapezoidem, w którym nierównoległe boki nie są równe długości. Oznacza to, że mają nogi o dwóch różnych długościach.
Formuła pola trapezowego
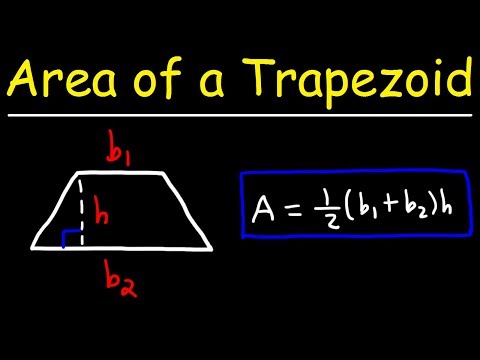
Aby znaleźć obszar trapezu, możesz użyć następującego równania:
Obszar = ((b1 + b2) / 2) * godz
b1 i b2 są długościami dwóch baz na trapezie; h jest równa wysokości trapezu, czyli długości od dolnej podstawy do górnej linii podstawowej.
Nie zawsze podajesz wysokość trapezu. W takim przypadku często można ustalić wysokość za pomocą twierdzenia Pitagorasa.
Jak obliczyć powierzchnię nieregularnego trapezu: podane wartości
Ten pierwszy przykład będzie stanowić problem, gdy znasz wszystkie wartości trapezu.
b1 = 4 cm
b2 = 12 cm
h = 8 cm
Po prostu podłącz liczby do wzoru pola trapezowego i rozwiąż.
A = ((b1 + b2) / 2) * godz
A = ((4 cm + 12 cm) / 2) * 8 cm
A = (16 cm / 2) * 8 cm
A = 8 cm * 8 cm = 64 cm2
Jak obliczyć powierzchnię nieregularnego trapezu: Znajdowanie wysokości nieregularnego trapezu
W innych problemach lub sytuacjach z nieregularnymi trapezoidami często podaje się tylko pomiary podstaw i nóg trapezu wraz z niektórymi kątami trapezu, co pozwala ci samodzielnie obliczyć wysokość, zanim będziesz mógł obliczyć powierzchnię.
Następnie możesz użyć długości i kątów, aby obliczyć wysokość trapezu za pomocą wspólnych reguł trójkątnych kątów.
Pomyśl o tym . . . rysując linię wysokości na trapezie w punkcie końcowym mniejszej długości podstawy do dłuższej długości podstawy, tworzysz trójkąt z tą linią jako jedną stroną, noga trapezu jako drugą stroną i odległość od punkt, w którym linia wysokości dotyka większej podstawy, do punktu, w którym podstawa styka się z nogą jako trzecia strona (patrz szczegółowy rysunek tutaj).
Powiedzmy, że masz następujące wartości (patrz zdjęcie na tej stronie):
b1 = 16 cm
b2 = 25 cm
noga 2 = 12 cm
Kąt między b2 a noga 2 = 30 stopni
Znajomość kątów i jednej z wartości długości boku oznacza, że możesz następnie użyć reguł sin i cos, aby znaleźć wysokość. Przeciwprostokątna byłaby równa nodze 2 (12 cm) i mamy kąty do obliczenia wysokości.
Użyjmy grzechu do znalezienia wysokości za pomocą podanego kąta 30 stopni, co sprawi, że wysokość będzie równa „przeciwnej” w równaniu grzechu:
sin (kąt) = wysokość / przeciwprostokątna
sin (30) = wysokość / 12 cm
sin (30) * 12 cm = wysokość = 6 cm
Teraz, gdy masz już wartość wysokości, możesz obliczyć powierzchnię za pomocą formuły powierzchni:
A = ((b1 + b2) / 2) * godz
A = ((16 cm + 25 cm) / 2) * 6 cm
A = (41 cm / 2) * 6 cm
A = 20,5 cm * 6 cm = 123 cm2