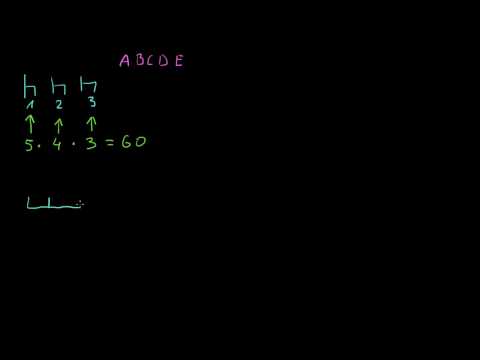
Zawartość
- Porządki i czynniki
- Permutacje z powtórzeniami
- Permutacje bez powtórzeń
- Kombinacje bez powtórzeń
- Kombinacje z powtórzeniami
Załóżmy, że masz n rodzajów przedmiotów i chcesz wybrać zbiór z nich. Możemy chcieć te przedmioty w określonej kolejności. Te zestawy elementów nazywamy permutacjami. Jeśli zamówienie nie ma znaczenia, nazywamy zestaw kombinacji kolekcji. Zarówno dla kombinacji, jak i permutacji, możesz rozważyć przypadek, w którym wybierasz niektóre typy n więcej niż jeden raz, który jest wywoływany z powtarzaniem lub przypadek, w którym wybierasz każdy typ tylko raz, co nazywa się brakiem powtórzeń. Celem jest policzenie liczby kombinacji lub kombinacji możliwych w danej sytuacji.
Porządki i czynniki
Funkcja silnia jest często używana podczas obliczania kombinacji i permutacji. N! oznacza N × (N – 1) × ... × 2 × 1. Na przykład 5! = 5 × 4 × 3 × 2 × 1 = 120. Liczba sposobów zamawiania zestawu elementów jest silnia. Weź trzy litery a, bi c. Masz trzy opcje na pierwszą literę, dwie na drugą i tylko jedną na trzecią. Innymi słowy, łącznie 3 × 2 × 1 = 6 zamówień. Ogólnie rzecz biorąc, istnieje n! sposoby zamawiania n produktów.
Permutacje z powtórzeniami
Załóżmy, że masz trzy pokoje, które zamierzasz pomalować, a każdy z nich zostanie pomalowany w jednym z pięciu kolorów: czerwony (r), zielony (g), niebieski (b), żółty (y) lub pomarańczowy (o). Możesz wybrać każdy kolor tyle razy, ile chcesz. Masz pięć kolorów do wyboru dla pierwszego pokoju, pięć dla drugiego i pięć dla trzeciego. Daje to w sumie 5 × 5 × 5 = 125 możliwości. Ogólnie rzecz biorąc, liczba sposobów na wybranie grupy r elementów w określonej kolejności spośród n powtarzalnych wyborów wynosi n ^ r.
Permutacje bez powtórzeń
Załóżmy teraz, że każdy pokój będzie miał inny kolor. Możesz wybrać jeden z pięciu kolorów dla pierwszego pokoju, czterech dla drugiego i tylko trzech dla trzeciego. Daje to 5 × 4 × 3 = 60, co akurat wynosi 5! / 2 !. Zasadniczo liczba niezależnych sposobów wyboru r elementów w określonej kolejności spośród n niepowtarzalnych wyborów wynosi n! / (N – r) !.
Kombinacje bez powtórzeń
Następnie zapomnij o tym, który pokój ma kolor. Wystarczy wybrać trzy niezależne kolory dla schematu kolorów. Kolejność nie ma tutaj znaczenia, więc (czerwony, zielony, niebieski) jest taki sam jak (czerwony, niebieski, zielony). Na każdy wybór trzech kolorów są 3! sposoby na ich zamówienie. Zmniejszasz więc liczbę permutacji o 3! aby uzyskać 5! / (2! × 3!) = 10. Ogólnie rzecz biorąc, możesz wybrać grupę r elementów w dowolnej kolejności spośród wybranych n niepowtarzalnych opcji na n! / sposoby.
Kombinacje z powtórzeniami
Na koniec musisz stworzyć schemat kolorów, w którym możesz użyć dowolnego koloru tyle razy, ile chcesz. Sprytny kod księgowy pomaga w tym zadaniu liczenia. Użyj trzech X do reprezentowania pokoi. Twoja lista kolorów jest reprezentowana przez rgbyo. Wmieszaj X do listy kolorów i skojarz każdy X z pierwszym kolorem po jego lewej stronie. Na przykład rgXXbyXo oznacza, że pierwszy pokój jest zielony, drugi jest zielony, a trzeci jest żółty. X musi mieć co najmniej jeden kolor po lewej stronie, więc jest pięć dostępnych miejsc dla pierwszego X. Ponieważ lista zawiera teraz X, istnieje sześć dostępnych miejsc dla drugiego X i siedem dostępnych miejsc dla trzeciego X. W wszystkie są 5 × 6 × 7 = 7! / 4! sposoby na napisanie kodu. Jednak kolejność pokoi jest dowolna, więc naprawdę jest tylko 7! / (4! × 3!) Unikalnych aranżacji. Ogólnie rzecz biorąc, możesz wybrać r elementów w dowolnej kolejności spośród n powtarzalnych wyborów na (n + r – 1)! / Sposoby.