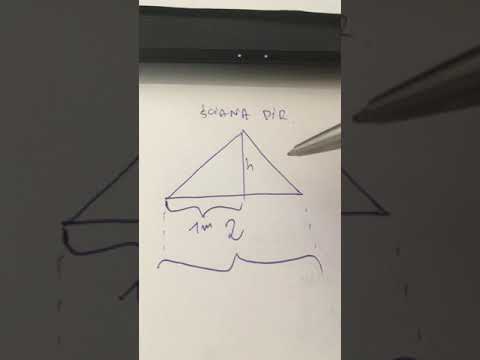
Używana w wielu budowlach, świątyniach i grobowcach na całym świecie kwadratowa piramida przyczyniła się do powstania niezliczonych budowli ludzkich. Piramidy są wielościanami (stałymi, trójwymiarowymi obiektami złożonymi z płaskich powierzchni i prostych krawędzi) i powstają, gdy podstawa i jej punkt, znany jako wierzchołek, są połączone trójkątami. Geometria, dział matematyki zajmujący się kształtami, rozmiarami i przestrzenią, oferuje rozwiązania pozwalające lepiej zrozumieć wymiary piramid. Obliczanie kątów piramidy odnosi się do kąta między dwoma sąsiadującymi trójkątnymi powierzchniami piramidy.
Określ długość trzeciego boku trójkąta przymocowanego zawiasowo do sąsiedniego trójkąta. Ze względu na kwadratową podstawę piramidy, która stanowi podstawę każdej powierzchni trójkąta, długość boku po przekątnej jest pierwiastkiem kwadratowym długości podstawy każdego trójkąta.
Oblicz obszar jednej z powierzchni trójkąta. Wszystkie trójkątne ściany piramidy powinny mieć takie same proporcje. Obszar można określić za pomocą prostej formuły: 1/2 podstawy (b) razy wysokość (h).
Zauważ, że prostopadła linia w dół pośrodku jednej z trójkątnych ścian tworzy dwa trójkąty prawe. Użyj twierdzenia Pitagorasa później, aby określić pozostałe kąty trójkąta.
Użyj wzoru 1 = 2bh / rootroot (b ^ 2 + 4h ^ 2), gdzie 1 jest wartością wysokości linii na trójkątnej powierzchni.
Użyj wzoru kwadratowy korzeń (2) b, aby określić długość podstawy trójkątnej powierzchni. Ponieważ musisz określić długość linii bazowej dla jednego z właściwych trójkątów, podziel tę liczbę na pół. Masz teraz dwie strony konieczne (przeciwprostokątna i podstawowa) do wypełnienia wspomnianego twierdzenia Pitagorasa.
Zastąp wartości (h) wysokości i (b) podstawy formułą: arcsin (rootroot (2) b / (2l)) = arcsin (sqrt (8h ^ 2 + 2b ^ 2) / 4h). To da ci kąt piramidy od wierzchołka do krawędzi podstawy.