Zawartość
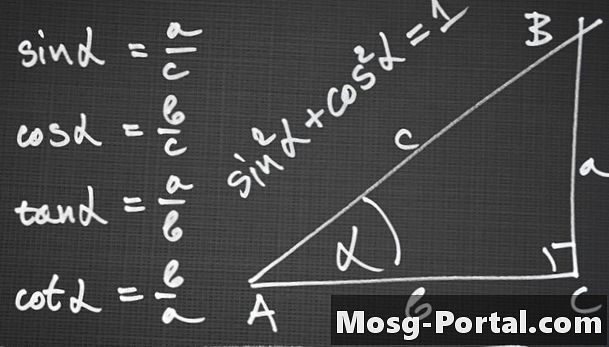
Prawo sinusów i prawo cosinusów są równaniami trygonometrycznymi, które odnoszą miary kątów trójkąta do długości jego boków. Wywodzą się z właściwości, że większe kąty w trójkątach mają proporcjonalnie większe przeciwległe strony. Użyj prawa sinusów lub prawa cosinusów, aby obliczyć długości boków trójkąta i czworokąta (czworokąt to zasadniczo dwa sąsiednie trójkąty), jeśli znasz miarę jednego boku, jednego kąta i jednego dodatkowego boku lub kąta.
Oblicz długości boków trójkąta
Znajdź cechy trójkąta. Dane są długościami boków i miarami kątów, które są już znane.Nie można znaleźć miary długości boków trójkąta, chyba że znasz miarę jednego kąta, jednego boku i albo drugiego boku, albo innego kąta.
Użyj gestów, aby ustalić, czy trójkąt jest trójkątem ASA, AAS, SAS lub ASS. Trójkąt ASA ma dwa kąty, jak również bok łączący dwa kąty. Trójkąt AAS ma dwa kąty i inny bok jak daje. Trójkąt SAS ma dwa boki jako dane, a także kąt utworzony przez dwa boki. Trójkąt ASS ma dwa boki i inny kąt niż daje.
Użyj prawa sinusów, aby utworzyć równanie dotyczące długości boków, jeśli jest to trójkąt ASA, AAS lub ASS. Prawo sinusów mówi, że stosunki sinusów kątów trójkątów i ich przeciwnych boków są równe: sin A / a = sin B / b = sin C / c, gdzie a, b i c są przeciwległymi bokami długości kątów Odpowiednio A, B i C.
Na przykład, jeśli wiesz, że dwa kąty to 40 stopni i 60 stopni, a strona łącząca je miała 3 jednostki długości, ustaw równanie sin 80/3 = sin 40 / b = sin 60 / c (znasz kąt przeciwny bok o długości 3 jednostek ma 80 stopni, ponieważ suma kątów trójkątów wynosi 180 stopni).
Użyj prawa cosinusów, aby utworzyć równanie odnoszące się do długości boków, jeśli jest to trójkąt SAS. Prawo cosinusów mówi, że c ^ 2 = a ^ 2 + b ^ 2 - 2ab_cos C. Innymi słowy, kwadrat długości boku c jest równy kwadratom pozostałych dwóch długości boków minus iloczyn tych dwóch boki i cosinus kąta przeciwnego do nieznanego boku. Na przykład, jeśli dwie strony miałyby 3 jednostki i 4 jednostki, a kąt wynosiłby 60 stopni, zapisałbyś równanie c ^ 2 = 3 ^ 2 + 4 ^ 2 - 3_4 * cos 60.
Rozwiąż zmienne w równaniach, aby znaleźć nieznane długości trójkątów. Rozwiązanie dla bw równaniu sin 80/3 = sin 40 / b daje wartość b = 3 sin 40 / sin 80, więc b wynosi około 2. Rozwiązanie dla cw równaniu sin 80/3 = sin 60 / c daje wartość c = 3 sin 60 / sin 80, więc c wynosi około 2,6. Podobnie, rozwiązanie dla cw równaniu c ^ 2 = 3 ^ 2 + 4 ^ 2 - 3_4_cos 60 daje wartość c ^ 2 = 25 - 6 lub c ^ 2 = 19, więc c wynosi około 4,4.
Oblicz czworoboczne długości boków
Narysuj przekątną przez czworokąt (wybierz przekątną, która nie zawiera żadnych miar kąta; na przykład, jeśli kąt A jest podany w czworoboku ABCD, narysuj przekątną łączącą B i D).
Użyj przyrządów, aby skonfigurować trójkąt ASA, SAS, AAS lub ASS. Pamiętaj, że suma kątów czworoboku wynosi 360 stopni, więc możesz znaleźć miarę czwartego kąta, jeśli znasz pozostałe trzy.
Użyj prawa sinusów, aby rozwiązać długości boków czworoboku, jeśli ustawisz trójkąt ASA, AAS lub ASS. Użyj prawa cosinusa, aby rozwiązać długości boków, jeśli ustawisz trójkąt SAS.