
Zawartość
Aby dwa kształty były zgodne, każdy musi mieć tę samą liczbę boków, a ich kąty muszą być takie same. Najłatwiejszym sposobem ustalenia, czy dwa kształty są zgodne, jest obrócenie jednego z nich, aż zrówna się z drugim, lub po prostu ułóż kształty jeden na drugim, aby sprawdzić, czy końce wystają. Jeśli nie możesz fizycznie przenieść kształtów, możesz użyć formuł, aby ustalić, czy kształty są zgodne.
Kongruent Circles
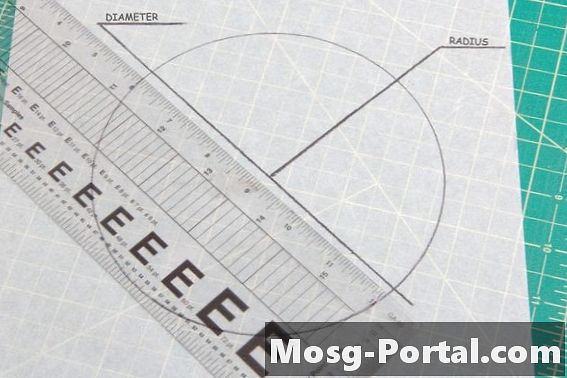
••• Ray Robert Green / Demand MediaWszystkie okręgi mają ten sam kąt 360 stopni. Jedynym czynnikiem określającym zgodność dwóch kręgów jest porównanie ich wielkości. Średnica jest linią prostą przechodzącą przez środek okręgu od krawędzi do krawędzi, zaś promień koła to długość od jego środka do zewnętrznej krawędzi. Pomiar jednego z nich w obu kręgach udowodni, czy są one zgodne.
Równoległoboki
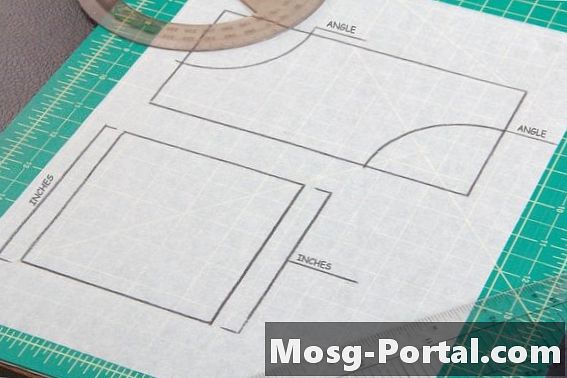
Równolegogram ma dwie pary równoległych boków, takich jak kwadraty i prostokąty. Przeciwległe boki lub kąty równoległoboku mają tę samą miarę, dlatego konieczne jest wykonanie dwóch pomiarów kąta lub boku na równoległoboku, po jednym z każdej pary boków, w celu porównania zgodności z innym kształtem.
Trójkąty
••• Ray Robert Green / Demand MediaAby znaleźć zgodność trójkątów, musisz określić rozmiar każdego kąta lub boku, ponieważ wszystkie trzy mogą być różne. Istnieją trzy postulaty, które można wykorzystać do identyfikacji przystających trójkątów. Postulat SSS dotyczy pomiaru wszystkich trzech boków każdego trójkąta. Postulat ASA mówi, że jeśli jakiekolwiek dwa kąty i ich strona łącząca są zgodne z kątem drugiego trójkąta, to są one zgodne. Postulat SAS robi coś przeciwnego, mierząc dwa boki i ich kąt połączenia w celu porównania z innym trójkątem.
Twierdzenia o przystających trójkątach

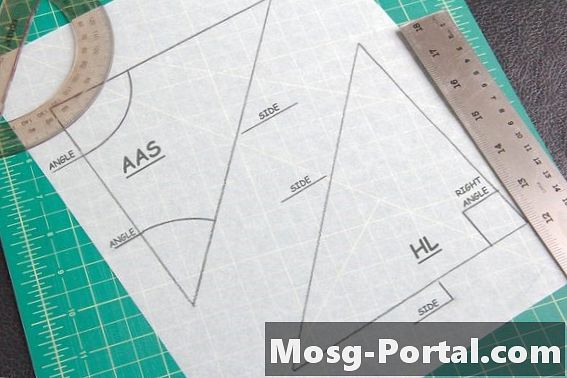
Dwa twierdzenia są przydatne do znalezienia przystających trójkątów. Twierdzenie AAS mówi, że jeśli dwa kąty i bok, który ich nie łączy, są równe kątowi innego trójkąta, to są one zgodne. Twierdzenie hipotenuenu i odnogi dotyczy tylko trójkątów o jednym kącie 90 stopni lub „prawo”. Dzieje się tak, gdy mierzy się przeciwprostokątną - stronę przeciwną do kąta 90 stopni - i jedną z pozostałych stron trójkąta, aby porównać z innym kształtem.