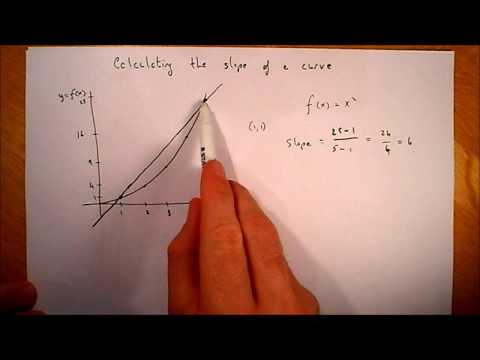
Aby obliczyć nachylenie krzywej, musisz obliczyć pochodną funkcji krzywych. Pochodna jest równaniem nachylenia linii stycznej do punktu na krzywej, którego nachylenie chcesz obliczyć. Jest to granica równania krzywych zbliżającego się do wskazanego punktu. Istnieje kilka metod obliczania pochodnej, ale reguła mocy jest najprostszą metodą i może być stosowana do większości podstawowych równań wielomianowych.
Napisz równanie krzywej. W tym przykładzie zastosowane zostanie równanie 3X ^ 2 + 4X + 6 = 0.
Skreślić dowolne stałe w pierwotnym równaniu. Nachylenie to szybkość zmiany, a ponieważ stałe się nie zmieniają, ich nachylenie wynosi 0, więc nie będą obecne w pochodnej.
Opuść moc każdego X terminu przed termin jako mnożnik i odejmij jedną z pierwotnej mocy, aby uzyskać nową moc. Tak więc 3X ^ 2 z przykładu staje się 2 (3X ^ 1) lub 6X, a 4X staje się 4. Te dwa kroki są podstawami reguły mocy. Przykładowe równanie pochodnej ma teraz wartość 6X + 4 = 0.
Wybierz punkt oryginalnej krzywej, którego nachylenie chcesz obliczyć, i podłącz współrzędną X do równania pochodnego, aby uzyskać wartość nachylenia. W przykładzie nachylenie w punkcie (1,16) wynosi 10.