Zawartość
Błąd standardowy średniej, znany również jako standardowe odchylenie średniej, pomaga określić różnice między więcej niż jedną próbką informacji. Obliczenia uwzględniają zmiany, które mogą występować w danych. Na przykład, jeśli weźmiesz wagę wielu próbek mężczyzn, pomiary mogą się znacznie różnić w każdej próbce; niektóre mogą ważyć 150 funtów, a inne 300 funtów. Jednak średnia z tych próbek będzie się różnić o zaledwie kilka funtów. Błąd standardowy średniej pokazuje, jak bardzo różne wagi różnią się od średniej.
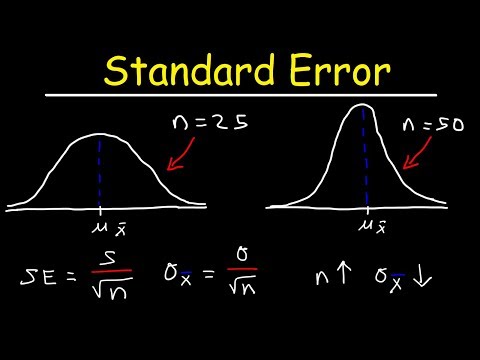
Napisz wzór σM = σ / √N, aby określić błąd standardowy średniej. W tym wzorze σM oznacza błąd standardowy średniej, liczby, której szukasz, σ oznacza odchylenie standardowe pierwotnego rozkładu, a √N jest kwadratem wielkości próbki.
Określ odchylenie standardowe pierwotnego rozkładu. Odchylenie standardowe mówi nam po prostu, jak daleko od siebie znajdują się liczby na linii liczbowej. Informacje mogą być dostarczone, jeśli pracujesz nad problemem statystycznym. Jeśli tak, zamień σ we wzorze na odchylenie standardowe. Jeśli nie zostanie podany, będziesz musiał go znaleźć na własną rękę.
Znajdź średnią swojego zestawu liczb, jeśli nie podano odchylenia standardowego; to znaczy, dodaj wszystkie liczby razem, a następnie podziel tę sumę przez liczbę dodanych elementów. Odejmij średnią z każdej z oryginalnych liczb i potęguj wyniki każdej z nich. Określ średnią tego nowego zestawu liczb, które wypracowałeś; odpowiedź da ci wariancję. Wyrównaj wariancję, aby znaleźć odchylenie standardowe. Podaj liczbę dla symbolu σ do formuły.
Określ wielkość próbki. Wielkość próbki to liczba elementów lub obserwacji, z którymi pracujesz. Zamień N we wzorze na wielkość próbki.
Znajdź pierwiastek kwadratowy wielkości próbki za pomocą kalkulatora.
Podziel odchylenie standardowe przez pierwiastek kwadratowy z wielkości próbki. Odpowiedź da ci standardowy błąd średniej.