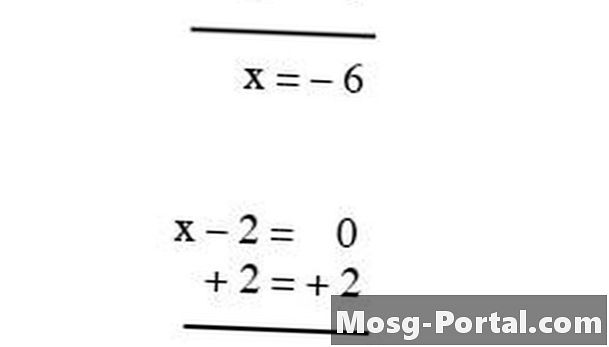
Zawartość
Równania faktoryzujące to jedna z podstaw algebry. Odpowiedź na złożone równanie można znaleźć o wiele łatwiej, dzieląc równanie na dwa proste równania. Chociaż proces ten może początkowo wydawać się trudny, w rzeczywistości jest dość prosty. Zasadniczo podzielisz równanie na dwie jednostki, które po pomnożeniu razem stworzą twój oryginalny przedmiot. Możesz rozkładać na czynniki i rozwiązywać równania w zaledwie kilku krokach.
Ustaw równanie na 0. Powiedzmy, że otrzymujesz równanie, takie jak x ^ 2 + 7x = --12, dodasz 12 po obu stronach równania, aby ustawić je na 0. Po wykonaniu tego równanie będzie wyglądało w ten sposób: x ^ 2 + 7x + 12 = 0.
Znajdź czynniki. W tym przypadku masz teraz do czynienia z x ^ 2 + 7x + 12 = 0. Można znaleźć współczynniki 12. Czynniki 12 obejmują 1, 2, 3, 4, 6 i 12.
Upewnij się, że twoje czynniki sumują się do środkowej zmiennej. Ze wszystkich czynników znalezionych w kroku 2 tylko 3 i 4 sumują się do 7, środkowej zmiennej. Kluczowe w faktoringu jest upewnienie się, że czynniki sumują się do zmiennej centralnej.
Uwzględnij nieznane zmienne. Ponieważ x jest podniesione do kwadratu, po uwzględnieniu go otrzymasz jeden x. Więcej informacji na temat postępowania z nieznanymi zmiennymi znajduje się w następnej sekcji.
Napisz swoje nowe równanie. Ponieważ 3 i 4 wydają się mieć rację, wypisz swoje równanie jako (x + 3) (x + 4) = 0.
Rozwiązać. Teraz możesz skonfigurować równanie do rozwiązania dla x. W tej sytuacji x + 3 = 0 i x + 4 = 0. Oba z nich pokazałyby, że x = --3 i x = --4.
Sprawdź swoje równanie, zastępując xs swoimi rozwiązaniami: --3 ^ 2 + 7 (- 3) + 12 = 0 9 + (--21) + 12 = 0 21 + (--21) = 0
--4^2 + 7(--4) + 12 = 0 16 + (--28) + 12 = 0 28 + (--28) = 0
Ustaw równanie na 0 i weź pod uwagę równanie, jak w krokach 1 i 2 ostatniej sekcji, jeśli twoje równanie ma ujemną wartość liczbową. Na przykład możesz otrzymać równanie takie jak x ^ 2 + 4x - 12 = 0.
Znajdź czynniki w x ^ 2 + 4x - 12 = 0. Dla tego równania współczynniki wynoszą 1, --1, 2, --2, 3, --3, 4, --4, 6, - 6, --12 i 12 dla liczby 12. Ponieważ ostatnia zmienna jest ujemna, jej czynniki będą dodatnie i ujemne. W tej sytuacji 6 i --2 będą twoimi czynnikami, ponieważ po pomnożeniu razem mają iloczyn --12, a po dodaniu razem ich iloczyn wynosi 4. Twoja odpowiedź będzie teraz wyglądać (x + 6) ( x - 2) = 0.
Rozwiąż dla x tak, jak to zrobiłeś w ostatniej sekcji; x wyniesie --6 i 2. Patrz rysunek 1.
Sprawdź swoje równanie, umieszczając swoje rozwiązania w miejscu x. (--6) ^ 2 + 4 (- 6) - 12 = 0 36 + (--24) - 12 = 0 36 + (--36) = 0
2^2 + 4(2) -- 12 = 0 4 + 8 -- 12 = 0 12 -- 12 = 0