Zawartość
W geometrii ośmiokąt jest wielokątem o ośmiu bokach. Zwykły ośmiokąt ma osiem równych boków i równych kątów. Zwykły ośmiokąt jest powszechnie rozpoznawany po znakach stop. Ośmiościan to ośmioboczny wielościan. Regularny ośmiościan ma osiem trójkątów o krawędziach równej długości. W rzeczywistości są to dwie kwadratowe piramidy spotykające się u ich podstaw.
Formula Octagon Area
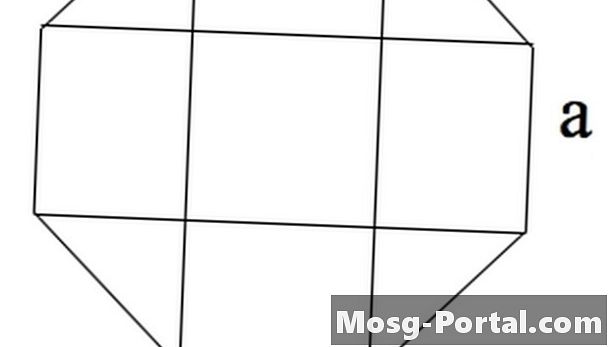
Wzór na powierzchnię regularnego ośmiokąta o bokach długości „a” wynosi 2 (1 + sqrt (2)) a ^ 2, gdzie „sqrt” oznacza pierwiastek kwadratowy.
Pochodzenie
Ośmiokąt można oglądać jako 4 prostokąty, jeden kwadrat w środku i cztery trójkąty równoramienne w rogach.
Kwadrat ma powierzchnię a ^ 2.
Trójkąty mają boki a, a / sqrt (2) i a / sqrt (2) według twierdzenia Pitagorasa. Dlatego każdy z nich ma powierzchnię ^ 2/4.
Prostokąty mają powierzchnię a * a / sqrt (2).
Suma tych 9 obszarów wynosi 2a ^ 2 (1 + sqrt (2)).
Formula Octahedron Volume
Wzór na objętość regularnego ośmiościanu boków „a” to ^ 3 * sqrt (2) / 3.
Pochodzenie
Obszar czterobocznej piramidy to obszar podstawy * wysokość / 3. Obszar regularnego ośmiokąta wynosi zatem 2 * podstawa * wysokość / 3.
Podstawa = a ^ 2 trywialnie.
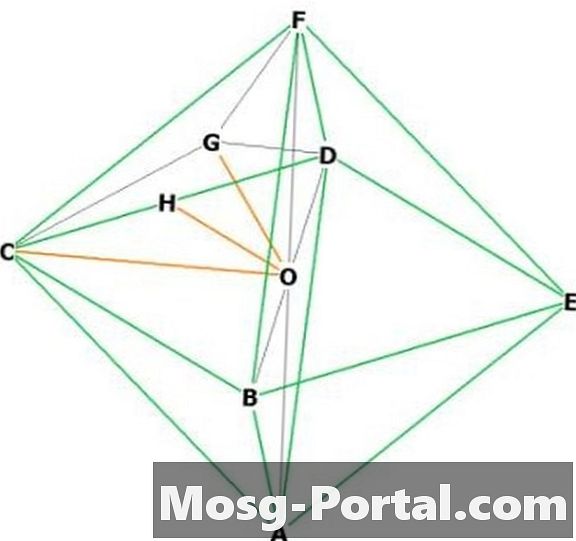
Wybierz dwa sąsiednie wierzchołki, powiedz „F” i „C.” „O” jest w centrum. FOC jest prostokątem równoramiennym o podstawie „a”, więc OC i OF mają długość a / sqrt (2) według twierdzenia Pitagorasa. Więc wysokość = a / sqrt (2).
Tak więc objętość zwykłego ośmiościanu wynosi 2 * (a ^ 2) * a / sqrt (2) / 3 = a ^ 3 * sqrt (2) / 3.
Powierzchnia
Powierzchnia regularnych ośmiościanów to obszar równobocznego trójkąta boków „a” razy 8.
Aby użyć twierdzenia Pitagorasa, upuść linię od wierzchołka do podstawy. Tworzy to dwa prawe trójkąty z przeciwprostokątną o długości „a” i jednej długości boku „a / 2”. Dlatego trzecią stroną musi być sqrt = sqrt (3) a / 2. Zatem obszar trójkąta równobocznego to wysokość * podstawa / 2 = sqrt (3) a / 2 * a / 2 = sqrt (3) a ^ 2/4.
Z 8 stron powierzchnia regularnego ośmiościanu wynosi 2 * sqrt (3) * a ^ 2.