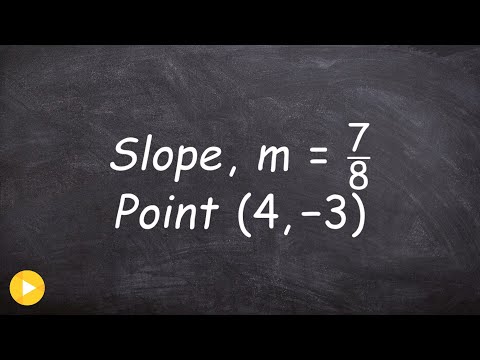
Zawartość
- Formularz nachylenia punktu zbicia
- Ponowne podsumowanie formularza przechwytywania nachylenia
- Konwersja nachylenia punktu na przechylenie nachylenia
Istnieją dwa konwencjonalne sposoby zapisu równania linii prostej. Jeden typ równania nazywa się formą punkt-nachylenie i wymaga znajomości (lub ustalenia) nachylenia linii i współrzędnych jednego punktu na linii. Drugi rodzaj równania nazywa się formą przechwytywania nachylenia i wymaga znajomości (lub ustalenia) nachylenia linii i współrzędnych jej y-przechwycić. Jeśli masz już linię punkt-nachylenie linii, wystarczy mała manipulacja algebraiczna, aby przepisać ją w postaci przechwytywania nachylenia.
Formularz nachylenia punktu zbicia
Zanim przejdziesz do konwertowania z formy punkt-nachylenie na formę punkt-nachylenie, oto krótkie podsumowanie tego, jak wygląda forma punkt-nachylenie:
y – y1 = m(x – x1)
Zmienna m oznacza nachylenie linii, a x1 i y1 są x i y współrzędne odpowiednio znanego punktu. Gdy zobaczysz linię w kształcie punktu-nachylenia z wypełnionymi współrzędnymi i nachyleniem, może to wyglądać mniej więcej tak:
y + 5 = 3(x – 2)
Zauważ, że y + 5 po lewej stronie równania jest równoważne z y - (-5), więc jeśli pomoże ci to rozpoznać równanie jako linię w postaci nachylenia punktu, możesz również zapisać to samo równanie, co:
y - (-5) = 3(x - 2)
Ponowne podsumowanie formularza przechwytywania nachylenia
Następnie krótkie podsumowanie tego, jak wygląda forma przechwytująca zbocze:
y = MX + b
Jeszcze raz, m reprezentuje nachylenie linii. Zmienna b oznacza y-_intercept linii lub, inaczej mówiąc, _x współrzędna punktu, w którym linia przecina y oś. Oto przykład rzeczywistej linii zapisanej w formie punktu przecięcia:
y = 5_x_ + 8
Konwersja nachylenia punktu na przechylenie nachylenia
Porównując dwa sposoby pisania linii, możesz zauważyć, że istnieją pewne podobieństwa. Oba zachowują a y zmienna, an x zmienna i nachylenie linii. Tak więc wszystko, czego naprawdę potrzebujesz, aby przejść od formy punkt-nachylenie do formy punkt-nachylenie, to trochę manipulacja algebraiczna. Rozważ podany przykład linii w formie nachylenia punktowego: y + 5 = 3(x – 2).
Użyj właściwości dystrybucyjnej, aby uprościć prawą stronę równania:
y + 5 = 3_x_ - 6
Odejmij 5 z obu stron równania, aby wyizolować y zmienna, która daje równanie w postaci nachylenia punktu:
y = 3_x_ - 11