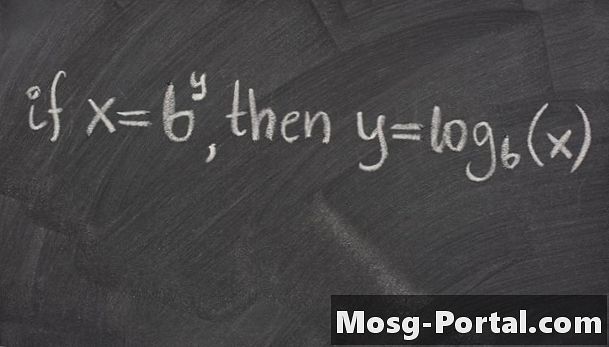
Zawartość
Logarytm jest funkcją matematyczną ściśle związaną z wykładnikami. W rzeczywistości logarytm jest odwrotnością funkcji wykładniczej. Ogólna forma to log_b (x), który brzmi „log log b” x. Często log bez bazy implikuje bazę 10 log log10, a ln odnosi się do „logu naturalnego” log_e, gdzie e jest ważną liczbą transcendentalną , e = 2,718282 .... Zasadniczo do obliczenia log_b (x) należy użyć kalkulatora, ale znajomość właściwości logarytmów może pomóc rozwiązać określone problemy.
Nieruchomości
Definicja podstawy logarytmicznej to log_b (b) = 1. Definicja funkcji logarytmicznej brzmi: jeśli y = b ^ x, to log_b (y) = x. Niektóre inne ważne właściwości to log_b (xy) = log_b (x) + log_b (y), log_b (x / y) = log_b (x) - log_b (y) i log_b (x ^ y) = ylog_b (x). Możesz użyć tych właściwości, aby pomóc obliczyć logarytmy w różnych sytuacjach.
Szybkie triki
Czasami możesz szybko obliczyć log_b (x), jeśli potrafisz rozwiązać problem b ^ y = x. Log_10 (1000) = 3, ponieważ 10 ^ 3 = 1000. Log_4 (16) = 2 ponieważ 4 ^ 2 = 16. Log_25 (5) = 0,5 ponieważ 25 ^ (1/2) = 5. Log_16 (1/2) = -1/4 ponieważ 16 ^ (- 1/4) = 1/2 lub (1/2) ^ 4 = 1/16. Korzystając ze wzoru log_b (xy), log_2 (72) = log_2 (8 * 9) = log_2 (8) + log_2 (9) = 3 + log_2 (9). Jeśli oszacujemy log_2 (9) ~ log_2 (8) = 3, to log_2 (72) ~ 6. Rzeczywista wartość to 6,2.
Zmiana baz
Załóżmy, że znasz log_b (x), ale chcesz poznać log_a (x). Nazywa się to zmienianiem zasad. Ponieważ a ^ (log_a (x)) = x, możesz napisać log_b (x) = log_b. Używając log_b (x ^ y) = ylog_b (x), możesz zmienić to w log_b (x) = log_a (x) log_b (a). Dzieląc obie strony przez log_b (a), możesz rozwiązać log_a (x): log_a (x) = log_b (x) / log_b (a). Jeśli masz kalkulator, który obsługuje 10 dzienników, ale chcesz poznać log_16 (7.3), możesz go znaleźć, log_16 (7.3) = log_10 (7.3) / log_10 (16) = 0,717.