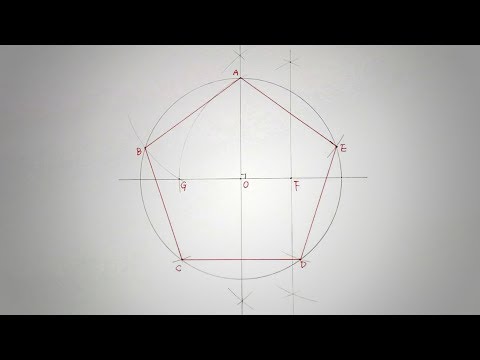
Najbardziej znaną postacią pięciokąta jest pięciokąt. Jego boki są równej długości, a każdy z jego wewnętrznych kątów wynosi 108 stopni. Artyści tacy jak Albrecht Dürer wraz z licznymi matematykami zaproponowali metody konstruowania pięciokątów. Korzystanie z papieru milimetrowego upraszcza proces, ułatwiając każdemu opanowanie kształtu.
Umieść punkt kompasu w rogu jednego z kwadratów w pobliżu środka papieru milimetrowego.
Odsuń ołówek od punktu na odległość 8 cm.
Narysuj okrąg i zaznacz środek „1”.
Postępuj zgodnie z linią na papierze milimetrowym w górę od „1” do góry koła. Oznacz ten punkt znakiem „A.”
Narysuj linię łączącą „1” i „A.”
Postępuj zgodnie z poziomą linią prowadzącą od „1” do krawędzi koła. Oznacz ten punkt znakiem „B.”
Zaznacz punkt „C” w połowie linii między „1” a „B.”
Umieść punkt kompasu na „C.” Porusz ramieniem tak, aby końcówka ołówka dotykała „A.” Narysuj okrąg.
Postępuj zgodnie z poziomą linią w lewo, aż przecina się z nowym okręgiem. Oznacz ten punkt znakiem „D.”
Umieść punkt kompasu na „A.”. Przesuń ramię, tak aby końcówka ołówka dotykała „D.”. Narysuj okrąg.
Zaznacz punkty, w których nowy okrąg styka się z pierwszym okręgiem, za pomocą „E” i „F.”
Umieść punkt kompasu na „E.”. Przesuń ramię, tak aby końcówka ołówka dotykała „A.”. Narysuj okrąg.
Zaznacz punkt, w którym koło dotyka oryginalnego koła, za pomocą „G.”
Umieść punkt kompasu na „F.”. Przesuń ramię, tak aby końcówka ołówka dotykała „A.”. Narysuj okrąg.
Zaznacz punkt, w którym koło styka się z oryginalnym okręgiem, za pomocą „H.”
Narysuj ciężką linię między „A” i „F”, używając linijki, aby utrzymać linię prostą. Następnie narysuj ciężką linię między „F” i „H”, „H” i „G”, „G” i „E” oraz „E” i „A.”